Elementary Structures of Matter
 |
 |
 |
| Author: |
Burkhard HEIM |
| Subject: |
Physics, relativity, unified field theory, elementary particles,
matter, |
| Abstract: |
A brief introduction into the very complex work of Burkhard
Heim is given. |
| Copyright: |
Copyright for Contents by Burkhard Heim, Northeim, 1998;
Translation by Prof. Dr. Hans Auerbach, Gebenstorf, 1998.
Copyright for HTML-Design: Bernhard Harrer, Berlin, 1999 |
| Info Jockey's Comment: |
This article has also been published in german
language. It is not yet easy to convert a text like this in HTML-format.
Nevertheless I am very glad to present you this english translation of
an article by Burkhard Heim. [IJBH] |
 |
 |
 |
|
28. Jul. 1999
|
| More Comments |
|
Elementary Structures
of Matter
In physics a number of approaches are possible
in order to try to arrive at a comprehensive, unified theory describing
a maximum number of observable phenomena.
One such possibility would be the geometrization
of physical structures described in the two volumes Elementarstrukturen
der Materie (Elementary Structures
of Matter) [1] and [2]. A clear advantage of this approach is the fact
that space and object are no longer foreign to each other. Instead, an
object now appears as a specific metric structure of space. A consequence
of this is the unity of field and field source. The first attempt at such
a geometrization, applied to the gravitational field, was carried out by
A. Einstein in his general theory of relativity, later on extended by Kaluza,
Klein, and Penrose, but also by P. Jordan and others.
The theory of supergravity and superstring
theory may be regarded as successors to the Kaluza–Klein model. At present,
superstring theory is being further developed in the hope of attaining
a unified description in a 10–dimensional space, R10 , of the
4 empirically known interactions. However, it is not clear how the predictions
of this theory, involving particle masses of some 1018 GeV,
can be verified in view of the limitations of present–day high energy experiments.
Here a radical geometrization of space as described in [1] and [2] appears
to lead to more suitable results that may readily be compared with observation.
An entirely different approach to the unified
description of nature by the use of group theoretical arguments has been
applied with some success to the unification of the 4 known elementary
forces. So far it has not also been possible to verify these theories experimentally,
again since the resulting mass spectrum of elementary particles involves
much too high energies. In addition, there is a lack of predictions concerning
quantum numbers of resonance spectra representing these masses and about
their upper limits.
By extending the ideas of Einstein, Kaluza,
Klein and Jordan the theory outlined in this report shows how to geometrize
in principle not only the gravitational field but the other force fields
as well. They appear as geometrical structures of spacetime, R4
, (a Minkowski space with x4 = ict) subject to the usual conservation
laws, and lead to a general non–Hermitian geometry in R4 . The
covariant components of the corresponding triple index symbols,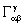 ,
representing generalized Christoffel symbols, can be split into a Hermitian
and an anti–Hermitian part, but, in contrast to Riemannian geometry, they
cannot in general be expressed explicitly in terms of derivatives of the
fundamental metric tensor, unless additional conditions are introduced.
However, since such conditions reduce the generality it is not known whether
they are at all admissible from a physical point of view. Thus, the
,
representing generalized Christoffel symbols, can be split into a Hermitian
and an anti–Hermitian part, but, in contrast to Riemannian geometry, they
cannot in general be expressed explicitly in terms of derivatives of the
fundamental metric tensor, unless additional conditions are introduced.
However, since such conditions reduce the generality it is not known whether
they are at all admissible from a physical point of view. Thus, the 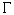 –symbols
are to be treated as components of a unified field of metric structures.
–symbols
are to be treated as components of a unified field of metric structures.
A transition to the microscopic region by use
of the correspondence principle turns the unified field components into
true tensor components with respect to the group of one–to–one, continuous,
and non–singular coordinate transformations (Poincare´–group), with
mixed covariant and contravariant indices. This also applies to the macroscopic
domain, where a unique set of metric structures corresponds to each type
of field (gravitational, e.m.). Different fields, characterized by different
conservation laws, lead to different geodetic conditions.
On passing over to the microscopic domain the 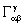 –symbols,
which are non– Hermitian in their covariant indices, transform into components
–symbols,
which are non– Hermitian in their covariant indices, transform into components 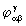 of a tensor field with mixed indices. The condition
of a tensor field with mixed indices. The condition 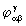 =
0 can only be satisfied if the corresponding R4 is completely
unstructured. In the microscopic range the phenomenological energy density
leads to a discrete set of eigenvalues and eigenfunctions,
=
0 can only be satisfied if the corresponding R4 is completely
unstructured. In the microscopic range the phenomenological energy density
leads to a discrete set of eigenvalues and eigenfunctions, 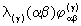 ,
characterizing a discrete spectrum of metric structures (parantheses around
,
characterizing a discrete spectrum of metric structures (parantheses around 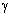 denote suspension of the summation convention). The concept of energy density
appears in geometrized form because phenomenological energies are time
derivatives of actions, so that spatial energy densities ultimately are
spacetime– dependent action densities. Hence, due to the quantization of
actions it is impossible in the limit to make the transition to differential
quotients. This implies the necessary existence of a smallest geometric
unit.
denote suspension of the summation convention). The concept of energy density
appears in geometrized form because phenomenological energies are time
derivatives of actions, so that spatial energy densities ultimately are
spacetime– dependent action densities. Hence, due to the quantization of
actions it is impossible in the limit to make the transition to differential
quotients. This implies the necessary existence of a smallest geometric
unit.
The nonlinear and non–Hermitian equations of
state satisfied by the R4 –structures 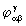 exhibit algebraic symmetries such that 28 out of the total of 43
= 64 relations for
exhibit algebraic symmetries such that 28 out of the total of 43
= 64 relations for 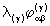 always
remain empty. Thus, 36 equations lead to relations
always
remain empty. Thus, 36 equations lead to relations 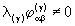 ,
while the empty level spectra of geometrical structures with
,
while the empty level spectra of geometrical structures with 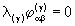 require that
require that 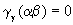 because
because  .
The fact that geometrical structures in the microscopic range vary in discrete
steps is the equivalent of the well–known discrete level structure of energy
densities, so that the 36 non–zero components must of necessity form a
tensor scheme having 6 rows and columns. In accordance with tensor algebra
this requires R4 to be a subspace of a 6–dimensional reference
space, R6 . The new coordinates, x5 and x6
, are imaginary, like x4.
.
The fact that geometrical structures in the microscopic range vary in discrete
steps is the equivalent of the well–known discrete level structure of energy
densities, so that the 36 non–zero components must of necessity form a
tensor scheme having 6 rows and columns. In accordance with tensor algebra
this requires R4 to be a subspace of a 6–dimensional reference
space, R6 . The new coordinates, x5 and x6
, are imaginary, like x4.
The appearance of two new coordinates indicates
that the limitation of quantum theory to 4 coordinates may be too restrictive.
After all, space and time are only aspects of human perception (I. Kant).
It should be mentioned that, since the R6 –coordinates are obtained
on the basis of conservation laws and energy relations, R6 must
be regarded as referring to the material world with x5 and x6
having to be interpreted as organizational
coordinates of material structures
in R4 .
A proof of existence shows that the eigenvalues 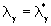 actually exist, but thereappears a further symmetry, indicating the vanishing
of an additional 12 of the remaining 36 components of the macroscopic energy
density tensor. These are the 4´3
spacelike elements occupying the upper half of columns 5 and 6 and the
left half of rows 5 and 6 of the tensor. This is to be expected on the
basis of macroscopic physics. Furthermore, it has led to the following
law governing the number of possible dimensions in hyperspace:
actually exist, but thereappears a further symmetry, indicating the vanishing
of an additional 12 of the remaining 36 components of the macroscopic energy
density tensor. These are the 4´3
spacelike elements occupying the upper half of columns 5 and 6 and the
left half of rows 5 and 6 of the tensor. This is to be expected on the
basis of macroscopic physics. Furthermore, it has led to the following
law governing the number of possible dimensions in hyperspace:
If p 0
dimensions of an Rp are empirically given, then there exists
a reference space Rn containing Rp , n being an integer,
such that the condition
0
dimensions of an Rp are empirically given, then there exists
a reference space Rn containing Rp , n being an integer,
such that the condition
(n–1)2 – 1 = p (p–1) (p–2)
is satisfied. For p = 0, 1, and 2 the positive
branch of this equation gives n = 2, while the negative branch gives n
= 0. However, the latter is irrelevant for all p > 2. Finally, the equation
is not satisfied for p = 3, p = 5, and all p > 6. For p = 4, on the other
hand, i.e. for spacetime, n actually turns out to equal 6. Furthermore,
for the material world, Rp , with p = 6, there exists a hyperspace
with n = 12, containing R 6 as subspace, which in turn contains
the subspace R4 . The concepts of energy and matter defined
in R 4 are no longer defined in the coordinates x7
... x12 , which again are imaginary, but the concept of volume
still is. The discussion in volumes [1] and [2] is confined to a semi–classical
treatment of the material world R 6 , because the nonlinear,
non–Hermitian R 4 –relations are readily transferred to R
6 , where they become completely Hermitian.
In order to derive the smallest geometric unit
mentioned above it is necessary to consider a universal background phenomenon.
A suitable quantity is the general inertia of all masses, which is always
equivalent to gravitational phenomena according to the principle of equivalence.
A phenomenological dynamics of gravitation is derived in [1], which, together
with a self–consistent treatment of the mass–equivalent of the gravitational
field energy, leads to the description of a scalar field function 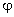 by
means of a non–linear system of equations, which formally agrees with the
nonlinear structural relations of R 6 . For constant x4 ,x5
, and x 6 the function
by
means of a non–linear system of equations, which formally agrees with the
nonlinear structural relations of R 6 . For constant x4 ,x5
, and x 6 the function 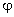 (x1
,...,x6
) then becomes
(x1
,...,x6
) then becomes 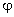 (x1
,x2 ,x3 )of R 3 .
(x1
,x2 ,x3 )of R 3 .
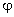 is a real, positive gravitational potential (potential energy per unit
mass), satisfying a nonlinear differential equation, which can be solved
in spherical geometry and results in a transcendental algebraic equation
for
is a real, positive gravitational potential (potential energy per unit
mass), satisfying a nonlinear differential equation, which can be solved
in spherical geometry and results in a transcendental algebraic equation
for 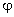 .
The solution shows that
.
The solution shows that 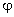 remains
real only between the limits R– and R+,
where R– corresponds to the Schwarzschild radius and
R+ to the Hubble radius. In the range
of relatively small distances (planetary systems)
remains
real only between the limits R– and R+,
where R– corresponds to the Schwarzschild radius and
R+ to the Hubble radius. In the range
of relatively small distances (planetary systems) 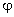 is
almost exactly proportional to 1/r and hence practically identical to Newton¢s
law of gravitation. This changes, however, in the range of very large distances,
because there exists a limit,
is
almost exactly proportional to 1/r and hence practically identical to Newton¢s
law of gravitation. This changes, however, in the range of very large distances,
because there exists a limit, 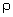 ,
of the attractive gravitational field, lying between R– and
R+ ,at
which
,
of the attractive gravitational field, lying between R– and
R+ ,at
which 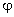 goes
to zero. This limit depends on the cube of the mean atomic weight of the
field source according to
goes
to zero. This limit depends on the cube of the mean atomic weight of the
field source according to 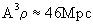 .
Beyond
.
Beyond 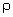 the
field becomes weakly repulsive before definitively going to zero at R+
.
the
field becomes weakly repulsive before definitively going to zero at R+
.
A single elementary particle is characterized
not only by 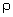 and
the limiting distances
and
the limiting distances 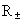 of its gravitational field, but also by its Compton wavelength. R–
vanishes in empty space when the mass of the field source approaches zero,
while R +,
of its gravitational field, but also by its Compton wavelength. R–
vanishes in empty space when the mass of the field source approaches zero,
while R +, 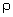 ,
and the Compton wavelength all diverge. However, since the smallest geometrical
unit must be a real number and a property of empty space its value has
to remain finite. As shown in [1], only a single product having this property
can be formed from the 4 characteristic lengths above. The result is an
area,
,
and the Compton wavelength all diverge. However, since the smallest geometrical
unit must be a real number and a property of empty space its value has
to remain finite. As shown in [1], only a single product having this property
can be formed from the 4 characteristic lengths above. The result is an
area, 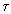 ,
bounded on all sides by geodesics, whose present size turns out to be 6.15´10
–70
m 2 . This quantity, called a metron,
represents the smallest area existing in empty space and requires the differential
calculus to be replaced by a calculus of finite areas. Accordingly, a whole
chapter in [1] is devoted to the development of a difference calculus considering
the finite area,
,
bounded on all sides by geodesics, whose present size turns out to be 6.15´10
–70
m 2 . This quantity, called a metron,
represents the smallest area existing in empty space and requires the differential
calculus to be replaced by a calculus of finite areas. Accordingly, a whole
chapter in [1] is devoted to the development of a difference calculus considering
the finite area, 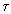 .
This enables any differential expression to be metronized. It follows that
in any subspace R n , whose dimensionality n is divisible by
2, the geometrical continuum is replaced by a metronic lattice formed by
n–dimensional volumes bounded on all sides by metrons. Thus, R 6
and R 12 are 6–dimensional and 12–dimensional metronic lattices,
respectively. Since all dimensions are metronized, even time proceeds in
finite, calculable steps. By the use of a difference calculus it becomes
possible to introduce
.
This enables any differential expression to be metronized. It follows that
in any subspace R n , whose dimensionality n is divisible by
2, the geometrical continuum is replaced by a metronic lattice formed by
n–dimensional volumes bounded on all sides by metrons. Thus, R 6
and R 12 are 6–dimensional and 12–dimensional metronic lattices,
respectively. Since all dimensions are metronized, even time proceeds in
finite, calculable steps. By the use of a difference calculus it becomes
possible to introduce 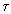 into the nonlinear system of geometric structures
in R 6 .
into the nonlinear system of geometric structures
in R 6 .
While the elementary areas 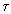 are always bounded by geodesics, their area remains constant in a deformed
lattice. The metronized state function then describes the projection of
a deformed R 6 –lattice into any Euclidian reference space,
where the metrons now appear in distorted or "condensed" form, in analogy
to the projection of a curved lattice onto a plane sheet, or to contour
lines of constant altitude on a map providing information on the structure
of a mountain range. In this respect there seems to exist a certain analogy
to Regge poles. The metronic system of equations itself has the character
of a selection principle, selecting out of a multiply infinite manifold
of possible R 6 –structures the ones whose projections into
R 4 describe elementary material processes of the physical world.
The operator performing this selection is called the "world selector".
are always bounded by geodesics, their area remains constant in a deformed
lattice. The metronized state function then describes the projection of
a deformed R 6 –lattice into any Euclidian reference space,
where the metrons now appear in distorted or "condensed" form, in analogy
to the projection of a curved lattice onto a plane sheet, or to contour
lines of constant altitude on a map providing information on the structure
of a mountain range. In this respect there seems to exist a certain analogy
to Regge poles. The metronic system of equations itself has the character
of a selection principle, selecting out of a multiply infinite manifold
of possible R 6 –structures the ones whose projections into
R 4 describe elementary material processes of the physical world.
The operator performing this selection is called the "world selector".
Further analysis shows that the world selector
separates out 4 sets of solutions, denoted by a,
b,
c,
and d,
involving 3 subspaces: A 2–dimensional subspace S 2 (x 5
,x 6 ), depending only on the two organizational coordinates,
a subspace T 1 (x 4 ), describing structures in time,
and a subspace R 3 (x 1 ,x 2 ,x 3
)
of physical space.
A different set of coordinates is involved
in each of the 4 structures a–d
mentioned
above: a
depends
on x 5 and x 6
, b
on
x 4 ,x 5 , and x 6 , c
on
x 1 ,x 2 ,x 3 ,x 5 , and x 6
, and d
depends
on all 6 coordinates x 1
,...,x 6 . In every one
of these combinations the coordinates are always grouped into subspaces
S 2 ,T 1 , and R 3 . Note that the organizational
coordinates x 5 and x 6 , constituting S 2
, appear in all elementary structures.
A sort of hermeneutics (from hermeneuo:
to interpret) of the world geometry,or hermetry
for
short, is required for interpreting the forms a
to
d
:
a
represents
structures outside of R
4 , which do not in general have a physical
interpretation. However, when projected into R 4 they appear as graviton
fields. The world lines belonging to elements of b
all
lie on the two–fold light cone in R 4 . For this reason they
always travel with the velocity of light in R 3 and are to be
interpreted as photons. In contrast to a
and
b,
hermetry forms c and
d
are
characterized by the inclusion of the real subspace R 3 , leading
to inertia and hence to rest mass. c
is
interpreted as referring to neutral particles, while d
refers
to charged ones. In the case of d a
coupling appearing between b and
c
characterizes
the charged condition. It was possible to derive a simple relationship
for an elementary charge determined by the quantum principle, whose numerical
value deviates by 0.125% from the experimental electron charge.
In addition, a general mass spectrum can be
derived, whose terms turn out to lie so close together that for all practical
purposes they approach a continuum. This is entirely due to the fact that
the spectrum is a superposition of energy terms of all
hermetry
forms. Thus, the practically continuous spectrum of the massless a–
and b–terms
is superimposed upon the discrete spectrum of hermetry forms c
and
d.
For this reason a "term selector" is required for separating out the discrete
mass spectra. Independently of this it is possible to derive the lower
bounds of spectra c and
d
and
to express them in terms of natural constants. They are R 3 –structures
representing the smallest masses, with d
yielding
the electron mass and c
resulting
in a neutral particle whose mass is about 0.1% smaller than that of the
electron.
As shown in [2], the upper reality bound, R
+
, of the gravitational field increases with diminishing
field source, i.e. the largest value of R, R max , results from the smallest
rest mass. Thus,  is the greatest possible distance in R 3 .It is defined in [2] as the diameter
of the universe and depends entirely on natural constants. These constants
disappear if the expression for
is the greatest possible distance in R 3 .It is defined in [2] as the diameter
of the universe and depends entirely on natural constants. These constants
disappear if the expression for 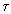 is substituted into the formula for R, and there
results a higher order algebraic expression for the dependence of D on
t,
referred to in [2] as the cosmological relation. Astrophysical reasons
require
is substituted into the formula for R, and there
results a higher order algebraic expression for the dependence of D on
t,
referred to in [2] as the cosmological relation. Astrophysical reasons
require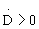 ,
where
,
where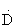 .
is the time derivative, which in turn results in
.
is the time derivative, which in turn results in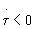 . Thus, as cosmic time progresses the metronic mesh size shrinks, while
the universe expands.
. Thus, as cosmic time progresses the metronic mesh size shrinks, while
the universe expands.
Going back in time, D decreases while 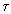 increases. This ends when
increases. This ends when 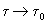 encompasses a "proto universe", whose diameter, D 0 , is given
by
encompasses a "proto universe", whose diameter, D 0 , is given
by 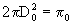 .
Since
.
Since 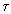 cannot
become smaller, this represents an initial event in R 4 , beyond
which there is no past. This instant has, therefore, been defined as the
moment t = 0 of the origin of the universe. By employing an appropriate
substitution D(
cannot
become smaller, this represents an initial event in R 4 , beyond
which there is no past. This instant has, therefore, been defined as the
moment t = 0 of the origin of the universe. By employing an appropriate
substitution D(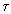 )
becomes the solution of a 7th order algebraic equation. At t = 0 and at
the end of time,
)
becomes the solution of a 7th order algebraic equation. At t = 0 and at
the end of time, 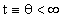 the equation has 3 real positive, 3 real negative, and one complex solution
for D. The positive solutions are interpreted as the diameters of 3 primordial
spheres emerging and expanding, one after the other, after t = 0. The spheres
mark the boundaries of the expanding universe, their calculated separations
in time shrinking to very small values, but never to zero, as cosmic time
advances. After D reaches a maximum value, contraction sets in. Finally,
at the end of time the trinity of spheres, now having diameters corresponding
to the 3 negative solutions, disappear one after another.
the equation has 3 real positive, 3 real negative, and one complex solution
for D. The positive solutions are interpreted as the diameters of 3 primordial
spheres emerging and expanding, one after the other, after t = 0. The spheres
mark the boundaries of the expanding universe, their calculated separations
in time shrinking to very small values, but never to zero, as cosmic time
advances. After D reaches a maximum value, contraction sets in. Finally,
at the end of time the trinity of spheres, now having diameters corresponding
to the 3 negative solutions, disappear one after another.
A long time after the initiation of cosmic
motion at t = 0, presumably after the appearance of matter, a symmetry
break of global groups leads to the development of 3 structural units 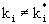 ,
i = 1,2,3,(k i is a 6´6
tensor) in the sense of tensorial integrands of integral operators. Tensor
multiplication and taking the trace according to the metronic difference
calculus results in generally non–Hermitian partial metric tensors g ij
= Tr(k i ´ k
j
) forming the elements of the full metric tensors,
,
i = 1,2,3,(k i is a 6´6
tensor) in the sense of tensorial integrands of integral operators. Tensor
multiplication and taking the trace according to the metronic difference
calculus results in generally non–Hermitian partial metric tensors g ij
= Tr(k i ´ k
j
) forming the elements of the full metric tensors, 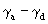 .
Since the 3 tensors k i are associated with the 3 primordial spheres, every
elementary particle retains a memory of the cosmic origin.
.
Since the 3 tensors k i are associated with the 3 primordial spheres, every
elementary particle retains a memory of the cosmic origin.
The structural units k i depend
on the hermetric subspaces of R 6 according to k1
(S2), k2(T1), and k3(R3).
Corresponding to the 4 hermetric forms a–d
one
can now form 4 generalized metric tensors 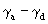 from
the partial tensors g defined above. If k1(S2), k2(T1),
and k3(R3) all differ from E (unit matrix) the resulting
from
the partial tensors g defined above. If k1(S2), k2(T1),
and k3(R3) all differ from E (unit matrix) the resulting 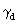 (S2,
T1, R3) depends on all 6 coordinates and represents
hermetry form d.
(S2,
T1, R3) depends on all 6 coordinates and represents
hermetry form d. 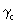 (S2,
R3), belonging to the spacelike hermetry form c,
is obtained by putting k2 (T1) = E. In similar manner
the timelike metric tensor,
(S2,
R3), belonging to the spacelike hermetry form c,
is obtained by putting k2 (T1) = E. In similar manner
the timelike metric tensor, 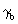 (S2
,T1 ), for hermetry form b
is
obtained by putting k3 (R3) = E. Finally,
(S2
,T1 ), for hermetry form b
is
obtained by putting k3 (R3) = E. Finally, 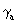 (S2)
for hermetry form a results
from k 2 (T 1 )=k 3 (R 3 )=E.
(S2)
for hermetry form a results
from k 2 (T 1 )=k 3 (R 3 )=E. 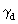 has
9 independent elements,
has
9 independent elements, 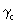 and
and 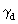 both
have 6, and
both
have 6, and 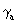 has
2, representing respectively 9–fold, 6–fold, and 2–fold metrics. These
polymetric structures combine to form the Hermitian metric field of the
"condensor", which is also Hermitian. The condensor is an operator projecting
a deformation in the 6–dimensional metronic lattice of R6 into
R4 , where it appears as an intricate, geometrically structured,
compressed or "condensed" lattice configuration. This condensed, structured
region is what we call matter constituting an elementary particle, as described
in more detail below.
has
2, representing respectively 9–fold, 6–fold, and 2–fold metrics. These
polymetric structures combine to form the Hermitian metric field of the
"condensor", which is also Hermitian. The condensor is an operator projecting
a deformation in the 6–dimensional metronic lattice of R6 into
R4 , where it appears as an intricate, geometrically structured,
compressed or "condensed" lattice configuration. This condensed, structured
region is what we call matter constituting an elementary particle, as described
in more detail below.
Thus, both the world selector and the condensor
describing the internal particle structure can be split up in a manner
allowing a system of partial metrics to be specified for each hermetric
form. An appropriate choice of indices (ij) then results in a solution
of the general energy spectrum corresponding to a separation of the discrete
spectra c and
d.
These solutions actually yield discrete spectra of inertial masses, showing
good agreement with measured particle and resonance spectra.
The following picture regarding the spectrum
of elementary particles found in high energy experiments emerges from the
theoretical analysis above:
Elementary particles having rest mass constitute
self–couplings of free energy. They are indeed elementary as far as their
property of having rest mass is concerned, but internally they possess
a very subtle, dynamic structure. For this reason they are "elementary"
only in a relative sense.
Actually, such a particle appears as an elementary
flow system in R6 (equivalent to energy flows) of primitive
dynamic units called protosimplexes,
which combine to form flux aggregates. The protosimplex flow is a circulatory,
periodic motion similar to an oscillation. A particle can only exist if
the flux period comprises at least one full cycle, so that the duration
of a particle¢s
stability is always expressible as an integer multiple of the flux period.
Every dynamical R 6 –structure possible constitutes a flux aggregate
described by a set of 6 quantum numbers. All of them, however, result from
a very simple basic symmetry, essentially determined by the configuration
number k, which can only assume the
values k = 1 and k = 2. The empirically introduced baryonic charge then
corresponds to k – 1, i.e. k = 1 refers to mesons and k = 2 to baryons.
The physically relevant parts of an R 6
–flux
aggregate are its k + 1 components in the
physical space, R 3 , which are enveloped by a metric field.
Thus, mesons contain two and baryons three components. Evidently, there
exists an analogy to the empirically formulated concept of quarks. If this
is true, then quarks are not fundamental particles but non–separable, quasi–corpuscular
subconstituents in R 3 of a mesonic or baryonic elementary particle.
In this picture the condition of quark "confinement" is unnecessary. The
significance of a possible "quantum chromodynamics" will have to be derived
on the basis of a unified description of possible interactions. This problem
is being investigated in [3].
Inertial mass originates in the protosimplexes,
i.e. in the basic building blocks of flux aggregates, which form the structures
of the k + 1
subconstituents in R 3 . They compose 4 concentric spherical
shell–like configuration zones maintaining a dynamical equilibrium, during
whose existence there appears a measurable particle mass. However, an attempt
to measure the mass of a subconstituent part by scattering experiments
will result in a very broad, variable bandwidth of measurements, because
such a mass depends on the instantaneous flux phase. The sum of the k +
1 subconstituent masses, on the other hand, is
constant and gives in essence the measurable particle mass. The relevant
quantity in this connection is the degree to which the 4 configuration
zones in R 3 are occupied by dynamic flux elements.
For k = 1 and k = 2 there are altogether 25
sets of 6 quantum numbers each, characterizing the occupation of configuration
zones and the corresponding invariant rest masses. The particles belonging
to these invariant basic patterns are in turn combined into several families
of spin isomorphisms, in which the spatial flux dynamics of the configuration
zones is in dynamic equilibrium.
In all these terms there exists a single basic
invariant framework of occupied zones, depending only on whether k = 1
or k = 2. When these occupation numbers are substituted into the mass formula
derived in [2] this reproduces the masses of electron and proton to very
good accuracy. The masses of all other ground states are produced with
similar accuracy. However, the mass formula contains ratios of coupling
constants, which could not at the time of writing of [2] be derived theoretically
and had to be adjusted to fit experiments carried out at CERN in 1974.
Only in [3] has it become possible to derive the coupling constants from
first principles. A revised set of particle masses will be calculated after
publication of [3].
It seems that the lifetime of a state depends
on the deviation of its configuration zone occupation from the framework
structure mentioned above. It is conceivable, in analogy to the optically
active isomers of organic chemistry, that there exist isomers with spatial
reflection symmetry also in the area of flux aggregates, giving rise to
variations in lifetime. Perhaps the two equal–mass components of the K0
–meson, 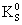 and
and 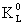 , are to be interpreted in this way.
, are to be interpreted in this way.
Finally, the requirement that empty space be
characterized by vanishing zonal occupations and electric charge states
leads to some masses in the case of k = 1, which may be interpreted as
masses of neutrino states. However, these refer neither to rest masses
nor to free field energies (in analogy to photons), but to quantum–like
"field catalysts", i.e. masses of particles able to catalyze nuclear reactions
that otherwise would not take place. They transfer group theoretical properties,
arising from the sets of quantum numbers, through physical space.
The formula derived in [2] for the spectrum
of elementary particles also depends on an integer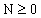 ,
where N = 0 refers to the 25 ground state masses. For N > 0 the sets of
quantum numbers again yield masses, which now denote resonance excitations
of the basic structural patterns to states of higher energy. According
to the dynamics of configuration zones only a single set of zonal occupations
is possible for each N. Evidently, the corresponding masses represent short–lived
resonance states, for all measured resonances appear among these spectra.
In each case N is limited, since for every set x of quantum numbers there
exists a finite resonance limit,
,
where N = 0 refers to the 25 ground state masses. For N > 0 the sets of
quantum numbers again yield masses, which now denote resonance excitations
of the basic structural patterns to states of higher energy. According
to the dynamics of configuration zones only a single set of zonal occupations
is possible for each N. Evidently, the corresponding masses represent short–lived
resonance states, for all measured resonances appear among these spectra.
In each case N is limited, since for every set x of quantum numbers there
exists a finite resonance limit, 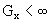 ,
such that the closed intervals
,
such that the closed intervals 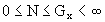 0
apply to every resonance order N, including the ground state. Out of the
relatively large number of logically possible particles, present–day high
energy accelerator experiments only record the small subset whose probabilities
of formation (depending on experimental conditions) is sufficiently large.
What evidently still is lacking is a general mathematical expression relating
these probabilities of formation to particle properties and experimental
boundary conditions. The theory developed in [1] and [2] represents a semi–classical
investigation. A third volume, entitled Strukturen
der physikalischen Welt und ihrer nichtmateriellen Seite (Structures
of the Physical World and its Non–Material Aspect), [3], leads beyond the
semi–classical domain to a dynamics in the hyperspace of R12.
0
apply to every resonance order N, including the ground state. Out of the
relatively large number of logically possible particles, present–day high
energy accelerator experiments only record the small subset whose probabilities
of formation (depending on experimental conditions) is sufficiently large.
What evidently still is lacking is a general mathematical expression relating
these probabilities of formation to particle properties and experimental
boundary conditions. The theory developed in [1] and [2] represents a semi–classical
investigation. A third volume, entitled Strukturen
der physikalischen Welt und ihrer nichtmateriellen Seite (Structures
of the Physical World and its Non–Material Aspect), [3], leads beyond the
semi–classical domain to a dynamics in the hyperspace of R12.
Burkhard Heim
Schillerstr. 2
D–37154 Northeim
[1] Heim, B. Elementarstrukturen
der Materie, Vol. 1 (revised), Resch
Verlag, Innsbruck, Austria, 1989
[2] Heim, B. Elementarstrukturen
der Materie, Vol. 2, Resch Verlag,
Innsbruck, Austria, 1984
[3] Dröscher, W., and Heim,
B. Strukturen der physikalischen Welt
und ihrer nichtmateriellen Seite, Resch
Verlag, Innsbruck, Austria, 1996
Layout: Datadiwan
eMail:webmeister@datadiwan.de